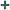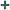aWc /ɛwawʃa/
|
information |
aWz /ɛwawza/
|
world; universe [ontology; general philosophy] ≈ DDC 110 |
a /ɛ/
|
forms; mathematical objects [formal sciences; logic; mathematics] ≈ DDC 510 160 |
a92 /ɛɲɔntɔ/ []
|
in neighbourhood |
a93 /ɛɲɔɲcɔ/ []
|
implied by; as a consequence of premise |
a94 /ɛɲɔŋkɔ/ []
|
with error |
a95 /ɛɲɔlpɔ/ []
|
through transformation; operation; function; map; morphism |
a96 /ɛɲɔltɔ/ []
|
having property |
a97 /ɛɲɔjɔ/ []
|
with part; element; component |
a98 /ɛɲɔrkɔ/ []
|
equal to result |
aat /ɛjɛta/
|
elements |
aau /ɛjɛu/
|
subsets |
aauc /ɛjɛuʃa/
|
structure-preserving subsets |
aaud /ɛjɛuda/
|
divisor subsets |
aauɭ /ɛjɛula/
|
lateral subsets |
aaun /ɛjɛuna/
|
independent subsets |
aauns /ɛjɛunasa/
|
bases ↞ akc vector spaces |
aaus /ɛjɛusa/
|
substructures |
aausq /ɛjɛusaca/
|
quotient-capable substructures |
aaw /ɛjɛwa/
|
cosets |
ab /ɛba/
|
individuals; instances |
ac /ɛʃa/
|
classes; sets; collections [set theory] |
ac97 /ɛʃaɲɔjɔ/ []
|
including; ⊃ subset |
ac98 /ɛʃaɲɔrkɔ/ []
|
containing; ∋ member; individual |
ac99 /ɛʃaɲɔɲɔ/ []
|
intensionality |
acai /ɛʃɛi/
|
intensionals fuzzy classes [fuzzy set theory; fuzzy logic] |
acaib /ɛʃɛiba/
|
not; other than; non-class |
acaie /ɛʃɛie/
|
hardly |
acaig /ɛʃɛiga/
|
almost; about quasi-class |
acaij /ɛʃɛiʒa/
|
scarcely; barely |
acaiɭ /ɛʃɛila/
|
little; a bit |
acain /ɛʃɛina/
|
partially |
acaiq /ɛʃɛica/
|
quite copula |
acais /ɛʃɛisa/
|
definitely; just |
acait /ɛʃɛita/
|
typically; stereotype; typical specimen |
acaiv /ɛʃɛiva/
|
very; extremely |
acan /ɛʃɛna/
|
occasionality |
acano /ɛʃɛno/
|
occasional; accidental attributes |
acans /ɛʃɛnasa/
|
by definition; substantial; essential; intrinsical substantial classes |
acb /ɛʃaba/
|
the empty class; empty set; nothing |
ae /ɛe/
|
relations; correspondences |
ae92 /ɛeɲɔntɔ/ []
|
in field |
ae923 /ɛeɲɔntɔɲcɔ/ []
|
from domain |
ae928 /ɛeɲɔntɔrkɔ/ []
|
to range; image |
ae93 /ɛeɲɔɲcɔ/ []
|
from set of departure |
ae938 /ɛeɲɔɲcɔrkɔ/ []
|
to codomain; set of destination |
ae96 /ɛeɲɔltɔ/ []
|
relation property |
ae99 /ɛeɲɔɲɔ/ []
|
of argument; term |
aeab /ɛeɛba/
|
arity; adicity; dimension; number of arguments; places ↞ anai integers |
aeabb /ɛeɛbaba/
|
nullary |
aeabc /ɛeɛbaʃa/
|
unary; properties [truth logic] |
aeabd /ɛeɛbada/
|
binary; diadic; 2-place |
aeabe /ɛeɛbe/
|
ternary; triadic; 3-place |
aead /ɛeɛda/
|
cardinality |
aeadb /ɛeɛdaba/
|
one-to-one |
aeadd /ɛeɛdada/
|
one-to-many |
aeadm /ɛeɛdama/
|
many-to-one |
aeadn /ɛeɛdana/
|
many-to-many |
aeah /ɛeɛɣa/
|
reflexive |
aeaj /ɛeɛʒa/
|
symmetric |
aeaɭ /ɛeɛla/
|
transitive |
aean /ɛeɛna/
|
connected |
aeaq /ɛeɛca/
|
equivalent ↞ aeah reflexive aeaj symmetric aeal transitive |
aeb /ɛeba/
|
identity ↞ aeaq equivalent |
aeb99 /ɛebaɲɔɲɔ/ []
|
of term |
aee /ɛeje/
|
equality |
aef /ɛefa/
|
similarity |
aei /ɛei/
|
inequality |
aem /ɛema/
|
set membership; belonging |
aem99 /ɛemaɲɔɲɔ/ []
|
to class |
aem997 /ɛemaɲɔɲɔjɔ/ []
|
of instance |
aep /ɛepa/
|
parthood; part-whole; inclusion [mereology] |
aep99 /ɛepaɲɔɲɔ/ []
|
in whole |
aep997 /ɛepaɲɔɲɔjɔ/ []
|
of part |
aepp /ɛepapa/
|
proper part-whole |
aept /ɛepata/
|
overlap |
aepu /ɛepu/
|
underlap |
aes /ɛesa/
|
set inclusion; genus-species |
aes99 /ɛesaɲɔɲɔ/ []
|
in genus |
aes997 /ɛesaɲɔɲɔjɔ/ []
|
of species |
af /ɛfa/
|
predications [predicate logic] |
af99 /ɛfaɲɔɲɔ/ []
|
of class; feature |
af998 /ɛfaɲɔɲɔrkɔ/ []
|
about object |
ag /ɛga/
|
operations; transformations; maps; morphisms |
ag96 /ɛgaɲɔltɔ/ []
|
operation property |
ag98 /ɛgaɲɔrkɔ/ []
|
equal to result |
ag99 /ɛgaɲɔɲɔ/ []
|
of operand |
ag99kc /ɛgaɲɔɲɔkaʃa/
|
vector spaces |
ag99kt /ɛgaɲɔɲɔkata/
|
topological spaces; continous functions |
ag99ɭt /ɛgaɲɔɲɔlata/
|
categories; functors |
agai /ɛgɛi/
|
associative |
agam /ɛgɛma/
|
commutative |
agap /ɛgɛpa/
|
idempotent |
agh /ɛgaɣa/
|
homomorphisms |
agh99 /ɛgaɣaɲɔɲɔ/ []
|
of structure |
agh99ɭmm /ɛgaɣaɲɔɲɔlamama/
|
monoids |
agh99ɭo /ɛgaɣaɲɔɲɔlo/
|
groups |
agh99ɭr /ɛgaɣaɲɔɲɔlara/
|
rings |
agh99me /ɛgaɣaɲɔɲɔme/
|
order homomorphisms; order-preserving functions |
agh99mr /ɛgaɣaɲɔɲɔmara/
|
graphs |
agh99msm /ɛgaɣaɲɔɲɔmasama/
|
matroids |
aghe /ɛgaɣe/
|
epimorphisms; surjective morphisms |
aghi /ɛgaɣi/
|
monomorphisms; injective morphisms |
aghm /ɛgaɣama/
|
isomorphisms; bijective morphisms ↞ aghe epimorphisms aghi monomorphisms |
aghn /ɛgaɣana/
|
endomorphisms |
aghu /ɛgaɣu/
|
automorphisms ↞ aghm isomorphisms aghn endomorphisms |
agm /ɛgama/
|
sum; union; addition |
agm98 /ɛgamaɲɔrkɔ/ []
|
equal to sum |
agm99 /ɛgamaɲɔɲɔ/ []
|
of term; addend; summand |
agm99kt /ɛgamaɲɔɲɔkata/
|
topological spaces; topologies |
agm99me /ɛgamaɲɔɲɔme/
|
posets |
agm99msm /ɛgamaɲɔɲɔmasama/
|
matroids |
agm99n /ɛgamaɲɔɲɔna/
|
quantities; numbers |
agm99nnr99nnq98nnt /ɛgamaɲɔɲɔnanaraɲɔɲɔnanacaɲɔrkɔnanata/ ⋄
|
2 + 3 = 5 |
agmd /ɛgamada/
|
disjoint union |
agmo /ɛgamo/
|
ordinal sum |
agn /ɛgana/
|
difference; complement; subtraction |
agn98 /ɛganaɲɔrkɔ/ []
|
equal to difference |
agn99 /ɛganaɲɔɲɔ/ []
|
of minuend |
agn993 /ɛganaɲɔɲɔɲcɔ/ []
|
minus subtrahend |
agn99n /ɛganaɲɔɲɔna/
|
quantities; numbers |
agn99nnt993nnq98nnr /ɛganaɲɔɲɔnanataɲɔɲɔɲcɔnanacaɲɔrkɔnanara/ ⋄
|
5 - 2 = 3 |
agns /ɛganasa/
|
symmetric difference; exclusive or; xor |
ago /ɛgo/
|
direct-like operations |
agom /ɛgoma/
|
direct sum |
agom99 /ɛgomaɲɔɲɔ/ []
|
of structure |
agom99kc /ɛgomaɲɔɲɔkaʃa/
|
vector spaces |
agom99msm /ɛgomaɲɔɲɔmasama/
|
matroids |
agop /ɛgopa/
|
direct product |
agop99 /ɛgopaɲɔɲɔ/ []
|
of structure |
agop99ɭmm /ɛgopaɲɔɲɔlamama/
|
monoids |
agop99ɭo /ɛgopaɲɔɲɔlo/
|
groups |
agop99ɭt /ɛgopaɲɔɲɔlata/
|
categories |
agp /ɛgapa/
|
product; intersection |
agp99 /ɛgapaɲɔɲɔ/ []
|
of factor |
agp99n /ɛgapaɲɔɲɔna/
|
quantities; numbers |
agp99nnr99nnq98nnu /ɛgapaɲɔɲɔnanaraɲɔɲɔnanacaɲɔrkɔnanu/ ⋄
|
3 x 2 = 6 |
agpc /ɛgapaʃa/
|
Cartesian product; cross product |
agpc99 /ɛgapaʃaɲɔɲɔ/ []
|
of structure |
agpc99kt /ɛgapaʃaɲɔɲɔkata/
|
topological spaces; Cartesian topologies |
agpc99me /ɛgapaʃaɲɔɲɔme/
|
posets |
agpc99mr /ɛgapaʃaɲɔɲɔmara/
|
graphs |
agpe /ɛgape/
|
semidirect product |
agq /ɛgaca/
|
quotient; division; partition |
agqe /ɛgace/
|
Euclidean division; division with remainder |
agqe98 /ɛgaceɲɔrkɔ/ []
|
equal to quotient |
agqe986 /ɛgaceɲɔrkɔltɔ/ []
|
with remainder |
agqe99 /ɛgaceɲɔɲɔ/ []
|
of dividend |
agqe993 /ɛgaceɲɔɲɔɲcɔ/ []
|
by divisor |
agqe99oss993nr /ɛgaceɲɔɲɔosasaɲɔɲɔɲcɔnara/ ⋄
|
44 / 3 |
agqs /ɛgacasa/
|
quotient structure |
agqs99 /ɛgacasaɲɔɲɔ/ []
|
of |
agqs99kt /ɛgacasaɲɔɲɔkata/
|
topological spaces; topologies |
agt /ɛgata/
|
tensor-like operations |
agtp /ɛgatapa/
|
tensor product |
agtp99 /ɛgatapaɲɔɲɔ/ []
|
of structure |
agtp99mr /ɛgatapaɲɔɲɔmara/
|
graphs |
agu /ɛgu/
|
lexicographic product |
agu99 /ɛguɲɔɲɔ/ []
|
of structure |
agu99mr /ɛguɲɔɲɔmara/
|
graphs |
agw /ɛgawa/
|
exponentiation; power |
agw99 /ɛgawaɲɔɲɔ/ []
|
of base |
agw993 /ɛgawaɲɔɲɔɲcɔ/ []
|
raised to the power exponent |
agw99n /ɛgawaɲɔɲɔna/
|
quantities; numbers |
agw99nnq993nnr98nnw /ɛgawaɲɔɲɔnanacaɲɔɲɔɲcɔnanaraɲɔrkɔnanawa/ ⋄
|
23 = 8 |
agx /ɛgaxa/
|
nth root |
agx993 /ɛgaxaɲɔɲɔɲcɔ/ []
|
-th |
agx993nnq /ɛgaxaɲɔɲɔɲcɔnanaca/
|
square |
agx993nnr /ɛgaxaɲɔɲɔɲcɔnanara/
|
cube |
agx99nnx993nnq98nnr /ɛgaxaɲɔɲɔnanaxaɲɔɲɔɲcɔnanacaɲɔrkɔnanara/ ⋄
|
√9 = 3 |
agy /ɛgaɟa/
|
logarithm |
agy99 /ɛgaɟaɲɔɲɔ/ []
|
of |
agy993 /ɛgaɟaɲɔɲɔɲcɔ/ []
|
to; base |
agy993nnq /ɛgaɟaɲɔɲɔɲcɔnanaca/
|
2; binary logarithm |
agy993nnqU /ɛgaɟaɲɔɲɔɲcɔnanacuj/
|
e; natural logarithm |
agy993nop /ɛgaɟaɲɔɲɔɲcɔnopa/
|
10; common logarithm |
agy99nous993nnq98nnu /ɛgaɟaɲɔɲɔnousaɲɔɲɔɲcɔnanacaɲɔrkɔnanu/ ⋄
|
log264 = 6 |
aiWj /ɛiwawʒa/
|
discrete structures [discrete mathematics; combinatorics] |
ai /ɛi/
|
statements; propositions [classical logic] |
aia /ɛiɛ/
|
truth value |
aiad /ɛiɛda/
|
contradictory; paradoxical |
aiaf /ɛiɛfa/
|
false |
aiat /ɛiɛta/
|
true |
aii /ɛiji/
|
implication |
aii98 /ɛijiɲɔrkɔ/ []
|
is consequence |
aii99 /ɛijiɲɔɲɔ/ []
|
of premise |
aiq /ɛica/
|
equivalence |
ais /ɛisa/
|
subjective propositions [modal logic] |
aj /ɛʒa/
|
formal languages; theories |
ajo /ɛʒo/
|
recursively enumerated languages; type 0 languages |
ajp /ɛʒapa/
|
context-sensitive languages; type 1 languages |
ajq /ɛʒaca/
|
context-free languages; type 2 languages |
ajr /ɛʒara/
|
regular languages; type 3 languages |
ajt /ɛʒata/
|
formal theories |
ak /ɛka/
|
spaces |
akc /ɛkaʃa/
|
vector spaces |
akc97t /ɛkaʃaɲɔjɔta/
|
vectors |
akc97uc /ɛkaʃaɲɔjɔuʃa/
|
subspaces of vector spaces; hyperplanes |
akcɭ /ɛkaʃala/
|
algebras |
ake /ɛke/
|
tensor spaces |
akf /ɛkafa/
|
affine spaces |
akn /ɛkana/
|
unitary spaces |
akt /ɛkata/
|
topological spaces |
akt97t /ɛkataɲɔjɔta/
|
elements of topological spaces; points |
akt97u /ɛkataɲɔjɔu/
|
subspaces of topological spaces |
aktd /ɛkatada/
|
discrete topological spaces [discrete topology] |
aktm /ɛkatama/
|
metric spaces |
aktp /ɛkatapa/
|
compact spaces |
akts /ɛkatasa/
|
separable spaces |
aktso /ɛkataso/
|
T0 spaces; Kolmogorov spaces |
aktsp /ɛkatasapa/
|
T1 spaces; Fréchet spaces |
aktsq /ɛkatasaca/
|
T2 spaces; Hausdorff spaces |
aktsr /ɛkatasara/
|
T3 spaces; regular spaces |
aktss /ɛkatasasa/
|
T4 spaces; regular Hausdorff spaces |
aktw /ɛkatawa/
|
manifolds |
aktwd /ɛkatawada/
|
differentiable manifolds |
aktwds /ɛkatawadasa/
|
smooth manifolds |
aktwr /ɛkatawara/
|
Riemannian manifolds |
aɭ /ɛla/
|
algebraic structures [algebra; abstract algebra] ≈ DDC 512 |
aɭb /ɛlaba/
|
general algebraic systems [universal algebra] |
aɭgWy /ɛlagawawɟa/
|
group-like structures |
aɭg /ɛlaga/
|
non-closed group-like structures; non-total group-like structures |
aɭge /ɛlage/
|
semigroupoids |
aɭgp /ɛlagapa/
|
groupoids |
aɭi /ɛli/
|
non-associative group-like structures |
aɭim /ɛlima/
|
magmas |
aɭiq /ɛlica/
|
quasigroups |
aɭiu /ɛliu/
|
loops |
aɭm /ɛlama/
|
non-commutative group-like structures |
aɭme /ɛlame/
|
semigroups |
aɭmi /ɛlami/
|
inverse semigroups |
aɭmm /ɛlamama/
|
monoids |
aɭmm97t /ɛlamamaɲɔjɔta/
|
monoid elements |
aɭmm97u /ɛlamamaɲɔjɔu/
|
submonoids |
aɭo /ɛlo/
|
groups [group theory] |
aɭo97t /ɛloɲɔjɔta/
|
group elements |
aɭo97u /ɛloɲɔjɔu/
|
subgroups |
aɭob /ɛloba/
|
Abelian groups |
aɭoc /ɛloʃa/
|
cyclic groups |
aɭoe /ɛloe/
|
symmetric groups |
aɭog /ɛloga/
|
alternating groups |
aɭoh /ɛloɣa/
|
dihedral groups |
aɭom /ɛloma/
|
simple groups |
aɭoms /ɛlomasa/
|
sporadic groups |
aɭor /ɛlora/
|
free groups |
aɭos /ɛlosa/
|
solvable groups |
aɭou /ɛlou/
|
Lie groups |
aɭow /ɛlowa/
|
topological groups ↞ ams families of sets |
aɭr /ɛlara/
|
ring-like structures |
aɭr97t /ɛlaraɲɔjɔta/
|
ring elements |
aɭr97u /ɛlaraɲɔjɔu/
|
subrings |
aɭr97ud /ɛlaraɲɔjɔuda/
|
divisor subsets |
aɭr97uɭ /ɛlaraɲɔjɔula/
|
lateral subsets |
aɭre /ɛlare/
|
semirings |
aɭrj /ɛlaraʒa/
|
non-associative rings [non-associative algebra] |
aɭrn /ɛlarana/
|
non-unitary rings; rngs |
aɭrr /ɛlarara/
|
rings [ring theory; associative algebra] |
aɭrrc /ɛlararaʃa/
|
commutative rings [commutative algebra] |
aɭrre /ɛlarare/
|
Boolean rings |
aɭrrf /ɛlararafa/
|
unique factorization domains |
aɭrri /ɛlarari/
|
principal ideal domains |
aɭrrk /ɛlararaka/
|
division rings; skew fields |
aɭrrn /ɛlararana/
|
noetherian rings |
aɭrrr /ɛlararara/
|
Artinian rings |
aɭrru /ɛlararu/
|
Lie rings |
aɭrrx /ɛlararaxa/
|
fields; polynomials [field theory] |
aɭrrxn /ɛlararaxana/
|
number fields |
aɭrrxt /ɛlararaxata/
|
cyclotomic fields |
aɭt /ɛlata/
|
categories [category theory] ↞ ac classes alg non-closed group-like structures |
aɭt97u /ɛlataɲɔjɔu/
|
category subsets |
aɭtao /ɛlatɛo/
|
objects |
aɭtar /ɛlatɛra/
|
morphisms; arrows |
aɭtc /ɛlataʃa/
|
pre-additive categories |
aɭtdWy /ɛlatadawawɟa/
|
additive categories |
aɭte /ɛlate/
|
pre-Abelian categories |
aɭtɭ /ɛlatala/
|
Abelian categories |
aɭtx /ɛlataxa/
|
exact categories |
am /ɛma/
|
combinatorial structures [combinatorics] |
ame /ɛme/
|
posets; partially ordered sets [order theory] |
ame97t /ɛmeɲɔjɔta/
|
poset elements; vertices; nodes |
ame97u /ɛmeɲɔjɔu/
|
subposets |
ameap /ɛmeɛpa/
|
inverse posets; dual posets; dual operation |
amear /ɛmeɛra/
|
linear extension of posets |
ameav /ɛmeɛva/
|
vertically-indecomposable poset component |
ameax /ɛmeɛxa/
|
poset intervals |
amed /ɛmeda/
|
total orders |
amei /ɛmei/
|
series-parallel posets |
amek /ɛmeka/
|
graded posets |
amer /ɛmera/
|
reduced posets |
amev /ɛmeva/
|
vertically irreducible posets |
amɭ /ɛmala/
|
lattice-like structures |
amɭj /ɛmalaʒa/
|
join-semilattices |
amɭm /ɛmalama/
|
meet-semilattices |
amɭt /ɛmalata/
|
lattices |
amɭtc /ɛmalataʃa/
|
complete lattices |
amɭtm /ɛmalatama/
|
modular lattices |
amɭts /ɛmalatasa/
|
distributive lattices |
amr /ɛmara/
|
graph-like structures |
amr97u /ɛmaraɲɔjɔu/
|
subgraphs |
amraf /ɛmarɛfa/
|
strong product of graphs ↞ agp product |
amrag /ɛmarɛga/
|
zigzag product of graphs ↞ agp product |
amrah /ɛmarɛɣa/
|
rooted product of graphs ↞ agp product |
amrar /ɛmarɛra/
|
edges; arcs; lines |
amrav /ɛmarɛva/
|
vertices; nodes; points |
amraw /ɛmarɛwa/
|
graph bridges |
amrax /ɛmarɛxa/
|
connected component of graphs |
amray /ɛmarɛɟa/
|
graph clique |
amrd /ɛmarada/
|
directed graphs ↞ ae relations |
amrdo /ɛmarado/
|
oriented graphs |
amrdot /ɛmaradota/
|
tournaments |
amrn /ɛmarana/
|
undirected graphs |
amrns /ɛmaranasa/
|
simple graphs ↞ aeaj symmetric |
amry /ɛmaraɟa/
|
undirected hypergraphs |
ams /ɛmasa/
|
families of sets ↞ amry undirected hypergraphs |
amse /ɛmase/
|
Sperner families |
amsh /ɛmasaɣa/
|
Helly families |
amsm /ɛmasama/
|
matroids |
amsm97t /ɛmasamaɲɔjɔta/
|
matroid elements |
amsmad /ɛmasamɛda/
|
dual matroids |
amsmas /ɛmasamɛsa/
|
independent sets of matroids |
an /ɛna/
|
quantities; amounts; numbers ≈ DDC 513 |
an96 /ɛnaɲɔltɔ/ []
|
number property |
an98 /ɛnaɲɔrkɔ/ []
|
abundance |
anab /ɛnɛba/
|
quantifiers |
anabb /ɛnɛbaba/
|
negative ↞ anb negative quantities |
anabc /ɛnɛbaʃa/
|
no ↞ anc none |
anabe /ɛnɛbe/
|
very few; very little |
anabf /ɛnɛbafa/
|
few; little |
anabi /ɛnɛbi/
|
middle; average |
anabm /ɛnɛbama/
|
some; a few; positive plural |
anabu /ɛnɛbu/
|
many; much |
anabv /ɛnɛbava/
|
very many; many many; very much |
anaby /ɛnɛbaɟa/
|
all; the totality |
anad /ɛnɛda/
|
numerals; decimal digits |
anade /ɛnɛde/
|
-9 |
anadf /ɛnɛdafa/
|
-8 |
anadg /ɛnɛdaga/
|
-7 |
anadh /ɛnɛdaɣa/
|
-6 |
anadi /ɛnɛdi/
|
-5 |
anadj /ɛnɛdaʒa/
|
-4 |
anadk /ɛnɛdaka/
|
-3 |
anadɭ /ɛnɛdala/
|
-2 |
anadm /ɛnɛdama/
|
-1 |
anadn /ɛnɛdana/
|
-0 |
anado /ɛnɛdo/
|
0 |
anadp /ɛnɛdapa/
|
1 |
anadq /ɛnɛdaca/
|
2 |
anadr /ɛnɛdara/
|
3 |
anads /ɛnɛdasa/
|
4 |
anadt /ɛnɛdata/
|
5 |
anadu /ɛnɛdu/
|
6 |
anadv /ɛnɛdava/
|
7 |
anadw /ɛnɛdawa/
|
8 |
anadx /ɛnɛdaxa/
|
9 |
anae /ɛnɛe/
|
primes |
anag /ɛnɛga/
|
even numbers ↞ annq two |
anai /ɛnɛi/
|
integers [arithmetic; number theory] |
anak /ɛnɛka/
|
exponential rationals; Q |
anar /ɛnɛra/
|
reals; R; continuum |
anat /ɛnɛta/
|
imaginary numbers |
anau /ɛnɛu/
|
complex numbers |
anaw /ɛnɛwa/
|
transcendent numbers |
anb /ɛnaba/
|
negative quantities |
anbd /ɛnabada/
|
negative tens of billions or more; -10>9 |
anbdx /ɛnabadaxa/ []
|
negative hundreds of billions; -1011 |
anbdy /ɛnabadaɟa/ []
|
negative tens of billions; -1010 |
anbe /ɛnabe/ []
|
negative billions; -109 |
anbf /ɛnabafa/ []
|
negative hundreds of millions; -108 |
anbg /ɛnabaga/ []
|
negative tens of millions; -107 |
anbh /ɛnabaɣa/ []
|
negative millions; -106 |
anbi /ɛnabi/ []
|
negative hundreds of thousands; -105 |
anbj /ɛnabaʒa/ []
|
negative tens of thousands; -104 |
anbk /ɛnabaka/ []
|
negative thousands; -103 |
anbɭ /ɛnabala/ []
|
negative hundreds; -102 |
anbm /ɛnabama/ []
|
negative tens; -101 |
anbmj /ɛnabamaʒa/ ⋄
|
-4 tens |
anbmjɭ /ɛnabamaʒala/ ⋄
|
-42 |
anbn /ɛnabana/ []
|
negative units; -100 |
anbne /ɛnabane/
|
-9 |
anbnf /ɛnabanafa/
|
-8 |
anbng /ɛnabanaga/
|
-7 |
anbnh /ɛnabanaɣa/
|
-6 |
anbni /ɛnabani/
|
-5 |
anbnj /ɛnabanaʒa/
|
-4 |
anbnjɭ /ɛnabanaʒala/ ⋄
|
-4.2 |
anbnk /ɛnabanaka/
|
-3 |
anbnɭ /ɛnabanala/
|
-2 |
anbnm /ɛnabanama/
|
-1; minus one |
anc /ɛnaʃa/
|
none; no; zero |
andWy /ɛnadawawɟa/
|
positive quantities |
and /ɛnada/
|
less than billionths; 10-(>9) |
andw /ɛnadawa/ []
|
trillionths; pico-; p-; 10-12 |
andx /ɛnadaxa/ []
|
10-11 |
andy /ɛnadaɟa/ []
|
10-10 |
ane /ɛne/ []
|
billionths; nano-; n-; 10-9 |
anf /ɛnafa/ []
|
10-8 |
ang /ɛnaga/ []
|
10-7 |
anh /ɛnaɣa/ []
|
millionths; micro-; μ-; 10-6; 0.00000 |
ani /ɛni/ []
|
10-5; 0.0000 |
anj /ɛnaʒa/ []
|
10-4; 0.000 |
ank /ɛnaka/ []
|
thousandths; milli-; m-; 10-3; 0.00 |
anɭ /ɛnala/ []
|
hundredths; centi-; c-; 10-2; 0.0 |
anm /ɛnama/ []
|
tenths; deci-; d-; 10-1; 0. |
anms /ɛnamasa/ [] ⋄
|
0.4 |
ann /ɛnana/ []
|
units; 100 |
anno /ɛnano/
|
no unit; 0 |
annp /ɛnanapa/
|
one; a; single; 1 |
annq /ɛnanaca/
|
two; a pair; a couple; 2 |
annqU /ɛnanacuj/
|
e; base of natural logarithm; 2.71828... |
annr /ɛnanara/
|
three; 3 |
annrU /ɛnanaruj/
|
π; pi; 3.14... |
anns /ɛnanasa/
|
four; 4 |
annt /ɛnanata/
|
five; 5 |
annu /ɛnanu/
|
six; 6 |
annv /ɛnanava/
|
seven; 7 |
annw /ɛnanawa/
|
eight; 8 |
annx /ɛnanaxa/
|
nine; 9 |
ano /ɛno/
|
tens; deca-; da-; 10¹ |
anoX /ɛnoxaw/ []
|
number of tens |
anoo /ɛnojo/
|
no ten; less than ten |
anop /ɛnopa/
|
one ten |
anopX /ɛnopaxaw/ []
|
number of units beside one ten |
anopo /ɛnopo/
|
10; ten |
anopp /ɛnopapa/
|
11; eleven |
anopq /ɛnopaca/
|
12; twelve |
anopr /ɛnopara/
|
13; thirteen |
anops /ɛnopasa/
|
14; fourteen |
anopt /ɛnopata/
|
15; fifteen |
anopu /ɛnopu/
|
16; sixteen |
anopv /ɛnopava/
|
17; seventeen |
anopw /ɛnopawa/
|
18; eighteen |
anopx /ɛnopaxa/
|
19; nineteen |
anoq /ɛnoca/
|
two tens |
anoqo /ɛnoco/
|
20; twenty |
anoqp /ɛnocapa/
|
21 |
anoqq /ɛnocaca/
|
22 |
anoqr /ɛnocara/
|
23 |
anoqs /ɛnocasa/
|
24 |
anoqt /ɛnocata/
|
25 |
anoqu /ɛnocu/
|
26 |
anoqv /ɛnocava/
|
27 |
anoqw /ɛnocawa/
|
28 |
anoqx /ɛnocaxa/
|
29 |
anor /ɛnora/
|
three tens |
anos /ɛnosa/
|
four tens |
anot /ɛnota/
|
five tens |
anou /ɛnou/
|
six tens |
anov /ɛnova/
|
seven tens |
anow /ɛnowa/
|
eight tens |
anox /ɛnoxa/
|
nine tens |
anp /ɛnapa/
|
hundreds; hecto-; h-; 10² |
anpX /ɛnapaxaw/ []
|
number of hundreds |
anpp /ɛnapapa/
|
one hundred |
anppq /ɛnapapaca/ ⋄
|
one hundred and two tens |
anppqo /ɛnapapaco/ ⋄
|
one hundred twenty; 120 |
anpq /ɛnapaca/
|
two hundreds |
anpqo /ɛnapaco/ ⋄
|
two hundreds and zero tens |
anpqoo /ɛnapacojo/ ⋄
|
200 |
anpqooo /ɛnapacojojo/ ⋄
|
200.0 |
anpqos /ɛnapacosa/ ⋄
|
204 |
anpqost /ɛnapacosata/ ⋄
|
204.5 |
anq /ɛnaca/
|
thousands; kilo-; K-; 10³ |
anqp /ɛnacapa/
|
one thousand |
anr /ɛnara/
|
tens of thousands; myria-; 104 |
ans /ɛnasa/
|
hundreds of thousands; 105 |
ant /ɛnata/
|
millions; mega-; M-; 106 |
anu /ɛnu/
|
tens of millions; 107 |
anv /ɛnava/
|
hundreds of millions; 108 |
anw /ɛnawa/
|
billions; giga-; G-; 109 |
anx /ɛnaxa/
|
more than billions; 10>9 |
anxb /ɛnaxaba/
|
tens of billions; 1010 |
anxc /ɛnaxaʃa/
|
hundreds of billions; 1011 |
anxd /ɛnaxada/
|
trillions; tera-; T-; 1012 |
anxg /ɛnaxaga/
|
quadrillions; peta-; P-; 1015 |
anxj /ɛnaxaʒa/
|
quintillions; exa-; E-; 1018 |
anxk /ɛnaxaka/
|
1019 |
anxɭ /ɛnaxala/
|
1020 |
any /ɛnaɟa/
|
infinite; ∞ |
aq /ɛca/
|
functions; equations [calculus; analysis] ≈ DDC 515 |
aq98 /ɛcaɲɔrkɔ/ []
|
having values; range output |
aq99 /ɛcaɲɔɲɔ/ []
|
at x =; domain input |
aqb /ɛcaba/
|
constants |
aqc /ɛcaʃa/
|
real functions [real analysis] |
aqd /ɛcada/
|
integrals [measure; integration] |
aqe /ɛce/
|
functions of a complex variable |
aqf /ɛcafa/
|
potential [potential theory] |
aqg /ɛcaga/
|
several complex variables; analytic spaces |
aqh /ɛcaɣa/
|
special functions |
aqi /ɛci/
|
ordinary differential equations; ODEs |
aqj /ɛcaʒa/
|
partial differential equations; PDEs |
aqk /ɛcaka/
|
dynamical systems [ergodic theory] |
aqɭ /ɛcala/
|
difference equations; functional equations |
aqm /ɛcama/
|
sequences; series; summability |
aqn /ɛcana/
|
approximations; expansions |
aqo /ɛco/
|
sinusoidal basis functions [Fourier analysis] |
aqoat /ɛcoɛta/
|
Fourier transform |
aqp /ɛcapa/
|
basic waves [abstract harmonic analysis] |
aqq /ɛcaca/
|
integral transforms [operational calculus] |
aqr /ɛcara/
|
integral equations |
aqs /ɛcasa/
|
spaces of functions [functional analysis] |
aqt /ɛcata/
|
operators [operator theory] |
aqv /ɛcava/
|
variations [calculus of variations; optimal control] |
at /ɛta/
|
algorithms [numerical analysis] ≈ DDC 518 |
at98 /ɛtaɲɔrkɔ/ []
|
by equation |
at98i /ɛtaɲɔrkɔi/
|
ordinal differential equations |
au /ɛu/
|
probabilities [probability theory; statistics] ≈ DDC 519 |
au97 /ɛuɲɔjɔ/ []
|
among sample size; n |
au98 /ɛuɲɔrkɔ/ []
|
value 0. |
au98t /ɛuɲɔrkɔta/ ⋄
|
0.5; 50% |
au99 /ɛuɲɔɲɔ/ []
|
of event |
aw /ɛwa/
|
systems; wholes; networks [general systems theory; cybernetics] ≈ DDC 003 |
aw2 /ɛwantɔ/
|
in environment |
awad /ɛwɛda/
|
system dynamics |
awade /ɛwɛde/
|
passive reaction |
awadi /ɛwɛdi/
|
active action |
awadn /ɛwɛdana/
|
change in attitude |
awan /ɛwɛna/
|
constituents; interchangeable parts |
awao /ɛwɛo/
|
organs; differentiated parts; sublevels |
awas /ɛwɛsa/
|
order states |
awasd /ɛwɛsada/
|
order |
awash /ɛwɛsaɣa/
|
chaos |
awasm /ɛwɛsama/
|
complexity |
awaso /ɛwɛso/
|
organization |
awaw /ɛwɛwa/
|
mechanicity |
awawc /ɛwɛwaʃa/
|
reductionistic; mechanical |
awawr /ɛwɛwara/
|
emergent |
awawy /ɛwɛwaɟa/
|
holistic |
awg /ɛwaga/
|
aggregates |
awi /ɛwi/
|
integrates |
awiag /ɛwiɛga/ []
|
integration stages |
awiage /ɛwiɛge/
|
integrands |
awiagv /ɛwiɛgava/
|
disintegrands |
awiagx /ɛwiɛgaxa/
|
remains |
awɭ /ɛwala/
|
levels |
awɭ93 /ɛwalaɲɔɲcɔ/ []
|
emerging from; originated by; produced after; overformed on; depending on lower level [dynamic ontology; process ontology] |
awɭ96 /ɛwalaɲɔltɔ/ []
|
having emergent property |
awɭam /ɛwalɛma/
|
emergence |
awɭɭ /ɛwalala/
|
layers; overformed levels; integrative levels |
awɭs /ɛwalasa/
|
strata; overbuilt levels |
qo{acqua} /co{ɛʃacuɛ}/ ⋄
|
the word acqua |
Connected classes:
|
⌕ 0
|
as for; relating to perspective; aspect; bias; viewpoint; phase relationship; dimension γ ↞ ae |
⌕ 038
|
taking example; study case; sample; specimen ↞ ab |
⌕ 0609 [anab]
|
theory applicability |
⌕ 08109 [anab]
|
occurring |
⌕ 1
|
at position; time; sequential position ↞ ame |
⌕ 2
|
in; within situation; location; condition; context ↞ ae |
⌕ 209 [anab]
|
centrality |
⌕ 2869 [anad]
|
at altitude Km ↞ j99 |
⌕ 5
|
through; by change; transformation; process ↞ ag |
⌕ 509 [anab]
|
stability degree |
⌕ 51
|
developed through; by history; evolution ↞ ag |
⌕ 7
|
with part; subsystem; component; organ; structure ↞ aw |
⌕ 7089 [ann]
|
fraction value |
⌕ 709 [anab]
|
proportion |
⌕ 759 [anab]
|
structure change |
⌕ 769 [anab]
|
continuity |
⌕ 770
|
mechanicity ↞ awaw |
⌕ 7709 [anab]
|
mechanicity |
⌕ 779 [anab]
|
complexity degree |
⌕ 8
|
as; like form; pattern; measure [morphology] ↞ a |
⌕ 809 [acai]
|
intension |
⌕ 8189 [an]
|
duration s |
⌕ 819 [anab]
|
duration |
⌕ 8259 [anab]
|
growth rate |
⌕ 82679 [anab]
|
height ↞ g98267 |
⌕ 8269 [anab]
|
length; x axis |
⌕ 8279 [anab]
|
area ↞ g9827 |
⌕ 8289 [an]
|
volume m3 |
⌕ 829 [anab]
|
size ↞ g982 |
⌕ 8389 [an]
|
weight measure Kg ↞ g97 |
⌕ 839 [anab]
|
weight |
⌕ 8459 [anab]
|
temperature change |
⌕ 8489 [an]
|
temperature K ↞ g94 |
⌕ 849 [anab]
|
temperature |
⌕ 8589 [an]
|
velocity m/s ↞ g925 |
⌕ 859 [anab]
|
speed; rapidity |
⌕ 8789 [an]
|
number |
⌕ 879 [anab]
|
quantifier |
⌕ 9
|
of; being kind; type; differentia; specification ↞ aeabc |
⌕ a92 [a]
|
in neighbourhood |
⌕ a93 [a]
|
implied by; as a consequence of premise |
⌕ a94 [a]
|
with error |
⌕ a95 [ag]
|
through transformation; operation; function; map; morphism |
⌕ a96 [a]
|
having property |
⌕ a97 [aa]
|
with part; element; component |
⌕ a98 [a]
|
equal to result |
⌕ aauns
|
bases ↞ akc |
⌕ ac97 [a]
|
including; ⊃ subset |
⌕ ac98 [a]
|
containing; ∋ member; individual |
⌕ ac99 [acai]
|
intensionality |
⌕ ae92 [a]
|
in field |
⌕ ae923 [a]
|
from domain |
⌕ ae928 [a]
|
to range; image |
⌕ ae93 [a]
|
from set of departure |
⌕ ae938 [a]
|
to codomain; set of destination |
⌕ ae96 [aea]
|
relation property |
⌕ ae99 [a]
|
of argument; term |
⌕ aeab
|
arity; adicity; dimension; number of arguments; places ↞ anai |
⌕ aeaq
|
equivalent ↞ aeah aeaj aeal |
⌕ aeb
|
identity ↞ aeaq |
⌕ aeb99 [a]
|
of term |
⌕ aem99 [a]
|
to class |
⌕ aem997 [a]
|
of instance |
⌕ aep99 [a]
|
in whole |
⌕ aep997 [a]
|
of part |
⌕ aes99 [a]
|
in genus |
⌕ aes997 [a]
|
of species |
⌕ af99 [a]
|
of class; feature |
⌕ af998 [a]
|
about object |
⌕ ag96 [aga]
|
operation property |
⌕ ag98 [a]
|
equal to result |
⌕ ag99 [a]
|
of operand |
⌕ agh99 [a]
|
of structure |
⌕ aghm
|
isomorphisms; bijective morphisms ↞ aghe aghi |
⌕ aghu
|
automorphisms ↞ aghm aghn |
⌕ agm98 [a]
|
equal to sum |
⌕ agm99 [a]
|
of term; addend; summand |
⌕ agn98 [a]
|
equal to difference |
⌕ agn99 [a]
|
of minuend |
⌕ agn993 [a]
|
minus subtrahend |
⌕ agom99 [a]
|
of structure |
⌕ agop99 [a]
|
of structure |
⌕ agp99 [a]
|
of factor |
⌕ agpc99 [a]
|
of structure |
⌕ agqe98 [an]
|
equal to quotient |
⌕ agqe986 [an]
|
with remainder |
⌕ agqe99 [an]
|
of dividend |
⌕ agqe993 [an]
|
by divisor |
⌕ agqs99 [a]
|
of |
⌕ agtp99 [a]
|
of structure |
⌕ agu99 [a]
|
of structure |
⌕ agw99 [a]
|
of base |
⌕ agw993 [a]
|
raised to the power exponent |
⌕ agx993 [a]
|
-th |
⌕ agy99 [a]
|
of |
⌕ agy993 [a]
|
to; base |
⌕ aii98 [a]
|
is consequence |
⌕ aii99 [a]
|
of premise |
⌕ aɭow
|
topological groups ↞ ams |
⌕ aɭt
|
categories [category theory] ↞ ac alg |
⌕ amraf
|
strong product of graphs ↞ agp |
⌕ amrag
|
zigzag product of graphs ↞ agp |
⌕ amrah
|
rooted product of graphs ↞ agp |
⌕ amrd
|
directed graphs ↞ ae |
⌕ amrns
|
simple graphs ↞ aeaj |
⌕ ams
|
families of sets ↞ amry |
⌕ an96 [ana]
|
number property |
⌕ an98 [anab]
|
abundance |
⌕ anabb
|
negative ↞ anb |
⌕ anabc
|
no ↞ anc |
⌕ anag
|
even numbers ↞ annq |
⌕ anbdx [anad]
|
negative hundreds of billions; -1011 |
⌕ anbdy [anad]
|
negative tens of billions; -1010 |
⌕ anbe [anad]
|
negative billions; -109 |
⌕ anbf [anad]
|
negative hundreds of millions; -108 |
⌕ anbg [anad]
|
negative tens of millions; -107 |
⌕ anbh [anad]
|
negative millions; -106 |
⌕ anbi [anad]
|
negative hundreds of thousands; -105 |
⌕ anbj [anad]
|
negative tens of thousands; -104 |
⌕ anbk [anad]
|
negative thousands; -103 |
⌕ anbɭ [anad]
|
negative hundreds; -102 |
⌕ anbm [anad]
|
negative tens; -101 |
⌕ anbn [anad]
|
negative units; -100 |
⌕ andw [anad]
|
trillionths; pico-; p-; 10-12 |
⌕ andx [anad]
|
10-11 |
⌕ andy [anad]
|
10-10 |
⌕ ane [anad]
|
billionths; nano-; n-; 10-9 |
⌕ anf [anad]
|
10-8 |
⌕ ang [anad]
|
10-7 |
⌕ anh [anad]
|
millionths; micro-; μ-; 10-6; 0.00000 |
⌕ ani [anad]
|
10-5; 0.0000 |
⌕ anj [anad]
|
10-4; 0.000 |
⌕ ank [anad]
|
thousandths; milli-; m-; 10-3; 0.00 |
⌕ anɭ [anad]
|
hundredths; centi-; c-; 10-2; 0.0 |
⌕ anm [anad]
|
tenths; deci-; d-; 10-1; 0. |
⌕ anms [anad] ⋄
|
0.4 |
⌕ ann [anad]
|
units; 100 |
⌕ anoX [anad]
|
number of tens |
⌕ anopX [anad]
|
number of units beside one ten |
⌕ anpX [anad]
|
number of hundreds |
⌕ aq98 [an]
|
having values; range output |
⌕ aq99 [an]
|
at x =; domain input |
⌕ at98 [aq]
|
by equation |
⌕ au97 [an]
|
among sample size; n |
⌕ au98 [anad]
|
value 0. |
⌕ au99 [a]
|
of event |
⌕ awɭ93 [a]
|
emerging from; originated by; produced after; overformed on; depending on lower level [dynamic ontology; process ontology] |
⌕ awɭ96 [a]
|
having emergent property |
⌕ b
|
spacetime; space-time continuum; events; pacha ↞ alo |
⌕ bb98 [an]
|
lasting s duration |
⌕ bbX [an]
|
time years |
⌕ bbY
|
present, past and future ↞ an |
⌕ bc
|
space; extension [geometry; algebraic geometry; topology] ↞ ak |
⌕ bcX
|
dimensions ↞ ann |
⌕ bcb98 [an]
|
long m length |
⌕ bcc98 [an]
|
large m² area |
⌕ bccX [an]
|
number of sides; edges |
⌕ bccb98 [aq]
|
with equation [differential geometry; differential topology] |
⌕ bccs [an]
|
polygons with more than 17 edges |
⌕ bcd98 [an]
|
amounting to m³; big/small size; volume |
⌕ bcd987 [an]
|
deep m depth |
⌕ bcd988 [an]
|
high m height |
⌕ bcd989 [an]
|
wide m width |
⌕ bv98 [an]
|
velocity m/s2; v; speed |
⌕ bv985 [an]
|
acceleration m/s²; a |
⌕ cX
|
dimensionality ↞ an |
⌕ d91 [an]
|
lasting s average lifetime |
⌕ d96 [anab]
|
with spin |
⌕ d969 [an]
|
with isospin; isotopic spin; isobaric spin |
⌕ d97 [an]
|
in quanta |
⌕ d98 [anab]
|
with charge |
⌕ darɭ98 [an]
|
of brightness; intensity; amplitude |
⌕ e95 [an]
|
with A; ampere electric current; I ↞ daml |
⌕ e965 [an]
|
conducing S/m electrical conductivity ; σ |
⌕ e968 [anad]
|
with electronegativity in Pauling scale |
⌕ e98 [an]
|
atomic mass |
⌕ e983 [an]
|
dense g/cm3 density |
⌕ e987 [an]
|
weighing standard atomic weight; relative atomic mass; Ar |
⌕ e99 [an]
|
atomic number; Z ↞ dvt |
⌕ eXXa [anad]
|
charge; ionization; ion |
⌕ f94 [an]
|
needing kJ/mol potential barrier; energy barrier; activation energy Ea |
⌕ f955 [an]
|
rate of reaction |
⌕ f958 [an]
|
J; joule enthalpy change; ΔH; heat of reaction |
⌕ f96 [anab]
|
ionization |
⌕ f965 [an]
|
reactivity |
⌕ f983 [an]
|
weighing molecular weight |
⌕ f9837 [an]
|
dense g/cm3 density |
⌕ f984 [an]
|
melting at K melting point ↞ gl gs |
⌕ f985 [an]
|
boiling at K boiling point ↞ gg gl |
⌕ f987 [an]
|
solubility ↞ fU |
⌕ f99 [anab]
|
acidity |
⌕ f998 [an]
|
ph |
⌕ g91 [an]
|
at time t |
⌕ g92 [an]
|
at place |
⌕ g925 [an]
|
moving at m/s speed; velocity |
⌕ g9255 [an]
|
accelerating at m/s2 acceleration |
⌕ g927 [an]
|
at spatial coordinate z |
⌕ g928 [an]
|
at spatial coordinate y |
⌕ g929 [an]
|
at spatial coordinate x |
⌕ g932 [an]
|
at Pa; pascal pressure; P |
⌕ g933 [an]
|
subjected to N; newtons force ↞ d93 |
⌕ g935 [an]
|
performing J; joule work |
⌕ g94 [an]
|
at K; kelvin temperature [thermodynamics] |
⌕ g944 [an]
|
entropy |
⌕ g951 [an]
|
of milliseconds duration |
⌕ g958 [an]
|
of dB; decibels intensity |
⌕ g97 [an]
|
of Kg; kilograms mass; M |
⌕ g977 [an]
|
dense Kg/m3 density; ρ |
⌕ g979 [an]
|
weighing Kg; kilograms weight |
⌕ g982 [an]
|
of m3; cubic meters volume ↞ bd |
⌕ g9826 [an]
|
of m; meters length ↞ bcb |
⌕ g98267 [an]
|
of m height; z axis |
⌕ g98268 [an]
|
of m width; y axis |
⌕ g98269 [an]
|
of m length; x axis |
⌕ g9827 [an]
|
of m2; square meters area ↞ bc |
⌕ ganX [an]
|
frequency; pitch Hz |
⌕ h922 [an]
|
at distance from Earth light years |
⌕ h955 [anab]
|
rotating spin |
⌕ h9551 [an]
|
rotating in terrestrial days rotation period |
⌕ h9581 [an]
|
orbiting in terrestrial days revolution period |
⌕ h96 [an]
|
color index; B–V index; temperature |
⌕ h98 [an]
|
apparent magnitude; m; vmag |
⌕ h99 [an]
|
absolute magnitude; Mv |
⌕ ib94 [an]
|
tenacity |
⌕ ib95 [an]
|
radioactivity |
⌕ ib96 [ann]
|
hardness in Mohs scale |
⌕ ib983 [an]
|
specific gravity |
⌕ ib995 [anab]
|
diaphaneity; transparency; pellucidity |
⌕ j982 [an] ⋄
|
of Km2 size |
⌕ j99 [anad]
|
at altitude Km a.s.l.; terrain; relief |
⌕ j996 [anad]
|
sloping tens degrees |
⌕ jagX
|
dates; days ↞ an |
⌕ jaɭ93 [an]
|
mm/year average precipitations ↞ jaki |
⌕ jaɭ94 [an]
|
K average temperature ↞ g94 |
⌕ jaqX [anad]
|
Richter magnitude |
⌕ jsɭ982 [an]
|
measuring Km2 surface |
⌕ jsr958 [an]
|
of m3/s; cubic meters per second; cumec discharge, rate of volumetric flow, water flow |
⌕ m981 [an]
|
aged years; old age |
⌕ m987 [an]
|
weighing g weight |
⌕ osu96 [an]
|
of bits information content |
⌕ osu970 [anab]
|
redundancy |
⌕ osu971 [an]
|
of s; seconds duration |
⌕ qhau
|
lengths; quantities; chronemes ↞ anab |
⌕ rabX [anad]
|
millennia |
⌕ rabXX [anad]
|
centuries |
⌕ rabXXX [anad]
|
decades |
⌕ rabXXXX [anad]
|
years |
⌕ ragg
|
sincerity; truth ↞ ai |
⌕ raɭrn
|
numerology ↞ an |
⌕ s974 [anab]
|
including fraction |
⌕ u93 [an]
|
plus asset; income; price |
⌕ u94 [an]
|
minus liability; expenditure; cost |
⌕ u987 [an]
|
producing output |
⌕ w96 [anab]
|
quality |
⌕ xm957 [an]
|
with instrument part |
⌕ xm968 [ann]
|
number of pitch classes |
⌕ y969 [anab]
|
for target expertise; intellectual level |
⌕ yams
|
modeling; simulation ↞ yeu a |
⌕ yim
|
mathematics; maths ↞ a |
⌕ yiyg
|
philosophical logic ↞ a yimb |
⌕ ytc915 [an]
|
issued each days seriality; periodicity |