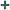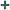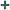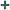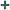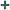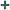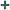ag /ɛga/
|
operations; transformations; maps; morphisms |
ag96 /ɛgaɲɔltɔ/ []
|
operation property |
ag98 /ɛgaɲɔrkɔ/ []
|
equal to result |
ag99 /ɛgaɲɔɲɔ/ []
|
of operand |
ag99kc /ɛgaɲɔɲɔkaʃa/
|
vector spaces |
ag99kt /ɛgaɲɔɲɔkata/
|
topological spaces; continous functions |
ag99ɭt /ɛgaɲɔɲɔlata/
|
categories; functors |
agai /ɛgɛi/
|
associative |
agam /ɛgɛma/
|
commutative |
agap /ɛgɛpa/
|
idempotent |
agh /ɛgaɣa/
|
homomorphisms |
agh99 /ɛgaɣaɲɔɲɔ/ []
|
of structure |
agh99ɭmm /ɛgaɣaɲɔɲɔlamama/
|
monoids |
agh99ɭo /ɛgaɣaɲɔɲɔlo/
|
groups |
agh99ɭr /ɛgaɣaɲɔɲɔlara/
|
rings |
agh99me /ɛgaɣaɲɔɲɔme/
|
order homomorphisms; order-preserving functions |
agh99mr /ɛgaɣaɲɔɲɔmara/
|
graphs |
agh99msm /ɛgaɣaɲɔɲɔmasama/
|
matroids |
aghe /ɛgaɣe/
|
epimorphisms; surjective morphisms |
aghi /ɛgaɣi/
|
monomorphisms; injective morphisms |
aghm /ɛgaɣama/
|
isomorphisms; bijective morphisms ↞ aghe epimorphisms aghi monomorphisms |
aghn /ɛgaɣana/
|
endomorphisms |
aghu /ɛgaɣu/
|
automorphisms ↞ aghm isomorphisms aghn endomorphisms |
agm /ɛgama/
|
sum; union; addition |
agm98 /ɛgamaɲɔrkɔ/ []
|
equal to sum |
agm99 /ɛgamaɲɔɲɔ/ []
|
of term; addend; summand |
agm99kt /ɛgamaɲɔɲɔkata/
|
topological spaces; topologies |
agm99me /ɛgamaɲɔɲɔme/
|
posets |
agm99msm /ɛgamaɲɔɲɔmasama/
|
matroids |
agm99n /ɛgamaɲɔɲɔna/
|
quantities; numbers |
agm99nnr99nnq98nnt /ɛgamaɲɔɲɔnanaraɲɔɲɔnanacaɲɔrkɔnanata/ ⋄
|
2 + 3 = 5 |
agmd /ɛgamada/
|
disjoint union |
agmo /ɛgamo/
|
ordinal sum |
agn /ɛgana/
|
difference; complement; subtraction |
agn98 /ɛganaɲɔrkɔ/ []
|
equal to difference |
agn99 /ɛganaɲɔɲɔ/ []
|
of minuend |
agn993 /ɛganaɲɔɲɔɲcɔ/ []
|
minus subtrahend |
agn99n /ɛganaɲɔɲɔna/
|
quantities; numbers |
agn99nnt993nnq98nnr /ɛganaɲɔɲɔnanataɲɔɲɔɲcɔnanacaɲɔrkɔnanara/ ⋄
|
5 - 2 = 3 |
agns /ɛganasa/
|
symmetric difference; exclusive or; xor |
ago /ɛgo/
|
direct-like operations |
agom /ɛgoma/
|
direct sum |
agom99 /ɛgomaɲɔɲɔ/ []
|
of structure |
agom99kc /ɛgomaɲɔɲɔkaʃa/
|
vector spaces |
agom99msm /ɛgomaɲɔɲɔmasama/
|
matroids |
agop /ɛgopa/
|
direct product |
agop99 /ɛgopaɲɔɲɔ/ []
|
of structure |
agop99ɭmm /ɛgopaɲɔɲɔlamama/
|
monoids |
agop99ɭo /ɛgopaɲɔɲɔlo/
|
groups |
agop99ɭt /ɛgopaɲɔɲɔlata/
|
categories |
agp /ɛgapa/
|
product; intersection |
agp99 /ɛgapaɲɔɲɔ/ []
|
of factor |
agp99n /ɛgapaɲɔɲɔna/
|
quantities; numbers |
agp99nnr99nnq98nnu /ɛgapaɲɔɲɔnanaraɲɔɲɔnanacaɲɔrkɔnanu/ ⋄
|
3 x 2 = 6 |
agpc /ɛgapaʃa/
|
Cartesian product; cross product |
agpc99 /ɛgapaʃaɲɔɲɔ/ []
|
of structure |
agpc99kt /ɛgapaʃaɲɔɲɔkata/
|
topological spaces; Cartesian topologies |
agpc99me /ɛgapaʃaɲɔɲɔme/
|
posets |
agpc99mr /ɛgapaʃaɲɔɲɔmara/
|
graphs |
agpe /ɛgape/
|
semidirect product |
agq /ɛgaca/
|
quotient; division; partition |
agqe /ɛgace/
|
Euclidean division; division with remainder |
agqe98 /ɛgaceɲɔrkɔ/ []
|
equal to quotient |
agqe986 /ɛgaceɲɔrkɔltɔ/ []
|
with remainder |
agqe99 /ɛgaceɲɔɲɔ/ []
|
of dividend |
agqe993 /ɛgaceɲɔɲɔɲcɔ/ []
|
by divisor |
agqe99oss993nr /ɛgaceɲɔɲɔosasaɲɔɲɔɲcɔnara/ ⋄
|
44 / 3 |
agqs /ɛgacasa/
|
quotient structure |
agqs99 /ɛgacasaɲɔɲɔ/ []
|
of |
agqs99kt /ɛgacasaɲɔɲɔkata/
|
topological spaces; topologies |
agt /ɛgata/
|
tensor-like operations |
agtp /ɛgatapa/
|
tensor product |
agtp99 /ɛgatapaɲɔɲɔ/ []
|
of structure |
agtp99mr /ɛgatapaɲɔɲɔmara/
|
graphs |
agu /ɛgu/
|
lexicographic product |
agu99 /ɛguɲɔɲɔ/ []
|
of structure |
agu99mr /ɛguɲɔɲɔmara/
|
graphs |
agw /ɛgawa/
|
exponentiation; power |
agw99 /ɛgawaɲɔɲɔ/ []
|
of base |
agw993 /ɛgawaɲɔɲɔɲcɔ/ []
|
raised to the power exponent |
agw99n /ɛgawaɲɔɲɔna/
|
quantities; numbers |
agw99nnq993nnr98nnw /ɛgawaɲɔɲɔnanacaɲɔɲɔɲcɔnanaraɲɔrkɔnanawa/ ⋄
|
23 = 8 |
agx /ɛgaxa/
|
nth root |
agx993 /ɛgaxaɲɔɲɔɲcɔ/ []
|
-th |
agx993nnq /ɛgaxaɲɔɲɔɲcɔnanaca/
|
square |
agx993nnr /ɛgaxaɲɔɲɔɲcɔnanara/
|
cube |
agx99nnx993nnq98nnr /ɛgaxaɲɔɲɔnanaxaɲɔɲɔɲcɔnanacaɲɔrkɔnanara/ ⋄
|
√9 = 3 |
agy /ɛgaɟa/
|
logarithm |
agy99 /ɛgaɟaɲɔɲɔ/ []
|
of |
agy993 /ɛgaɟaɲɔɲɔɲcɔ/ []
|
to; base |
agy993nnq /ɛgaɟaɲɔɲɔɲcɔnanaca/
|
2; binary logarithm |
agy993nnqU /ɛgaɟaɲɔɲɔɲcɔnanacuj/
|
e; natural logarithm |
agy993nop /ɛgaɟaɲɔɲɔɲcɔnopa/
|
10; common logarithm |
agy99nous993nnq98nnu /ɛgaɟaɲɔɲɔnousaɲɔɲɔɲcɔnanacaɲɔrkɔnanu/ ⋄
|
log264 = 6 |
Connected classes:
|
⌕ 5
|
through; by change; transformation; process ↞ ag |
⌕ 51
|
developed through; by history; evolution ↞ ag |
⌕ a95 [ag]
|
through transformation; operation; function; map; morphism |
⌕ ag96 [aga]
|
operation property |
⌕ aghm
|
isomorphisms; bijective morphisms ↞ aghe aghi |
⌕ aghu
|
automorphisms ↞ aghm aghn |
⌕ amraf
|
strong product of graphs ↞ agp |
⌕ amrag
|
zigzag product of graphs ↞ agp |
⌕ amrah
|
rooted product of graphs ↞ agp |